Difference between revisions of "MIRCdocument Display Goodies"
| Line 3: | Line 3: | ||
[[Image:MSTF.PNG|400px|right|Document Tab]] | [[Image:MSTF.PNG|400px|right|Document Tab]] | ||
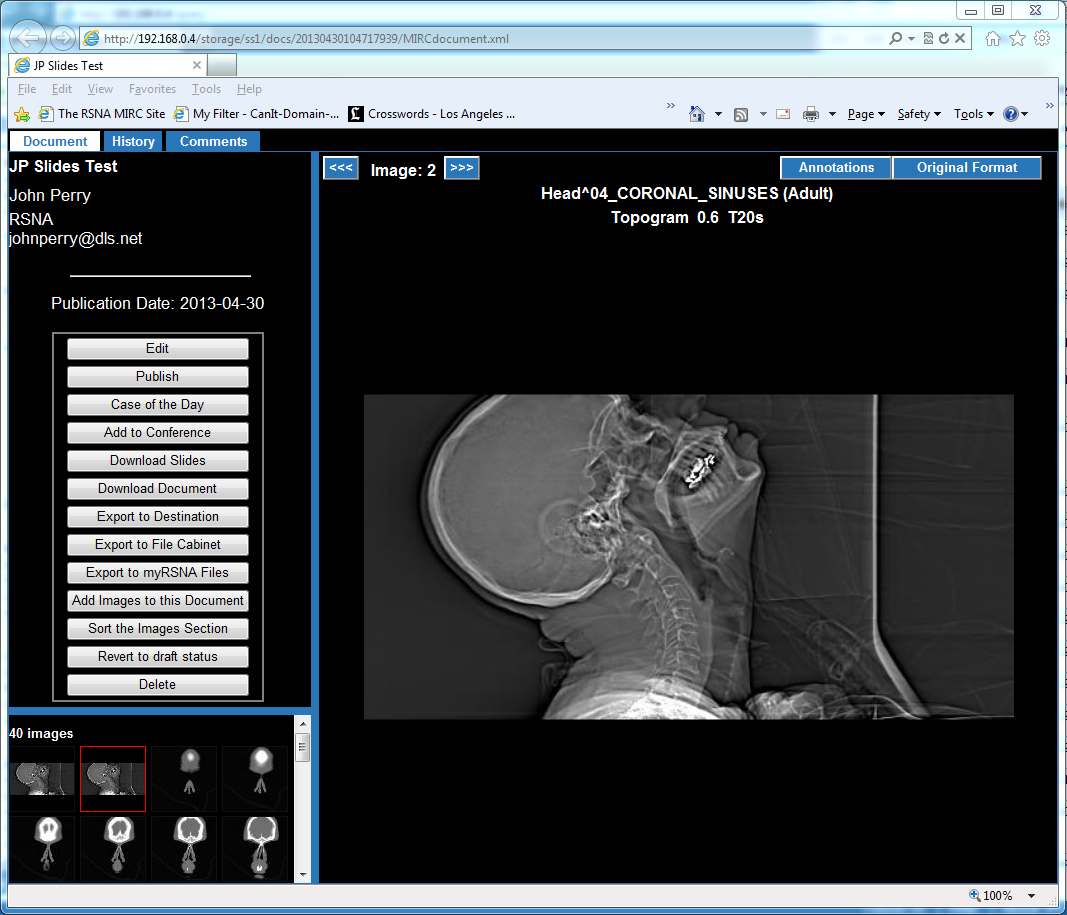
The most common MIRCdocument display format is called MSTF. It has a row of tabs across the top and three panes. The upper left pane displays the contents of the selected tab. The lower left pane displays token images representing all the images in the MIRCdocument. The right pane displays a single image. | The most common MIRCdocument display format is called MSTF. It has a row of tabs across the top and three panes. The upper left pane displays the contents of the selected tab. The lower left pane displays token images representing all the images in the MIRCdocument. The right pane displays a single image. | ||
| + | |||
| + | <b><font size=3>Resizing the Panes</font></b> | ||
| + | |||
| + | The panes may be resized by dragging the blue dividers. | ||
| + | |||
| + | The <b>PAGE UP</b> key moves the divider all the way to the left. | ||
| + | |||
| + | The <b>PAGE DOWN</b> key moves the divider back to the position it had when the <b>PAGE UP</b> key was pressed. If the <b>PAGE DOWN</b> key is pressed when the divider is not at the full left position, the divider resizes the pane to fit the image. | ||
Revision as of 12:28, 3 May 2013
This article describes the special features that are available for navigation in the display of a MIRCdocument. The features described are available in version Z130 and later.
The most common MIRCdocument display format is called MSTF. It has a row of tabs across the top and three panes. The upper left pane displays the contents of the selected tab. The lower left pane displays token images representing all the images in the MIRCdocument. The right pane displays a single image.
Resizing the Panes
The panes may be resized by dragging the blue dividers.
The PAGE UP key moves the divider all the way to the left.
The PAGE DOWN key moves the divider back to the position it had when the PAGE UP key was pressed. If the PAGE DOWN key is pressed when the divider is not at the full left position, the divider resizes the pane to fit the image.